October Rich Math Problem: Who is the Imposter?
Developed by Catherine Floyd and adapted from Christopher Danielson
Content Standards: Ratios and Proportions Relationships
6.RPA.1 Understand the concept of a ratio and use ratio language to describe a relationship between two quantities.
6.RPA.3A Make tables of equivalent ratios relating quantities with whole-number measurements, find missing values in the tables, and plot the pairs of values on the coordinate plane. Use tables to compare ratios.
7.RP.1 Compute unit rates associated with ratios of fractions, including ratios of lengths, areas, and other quantities measured in like or different units.
7.RP.2 Recognize and represent proportional relationships between quantities.
Math Process Standards (Common Core):
MP2 Reason abstractly and quantitatively.
MP3 Construct viable arguments and critique the reasoning of others.
MP7 Look for and make use of structure.
MP8 Look for and express regularity in repeated reasoning.
Introduction:
Purple paint can be created by mixing different proportions of the colors red and blue. The students are going to look at four different representations of combinations of purple paint. They will need to determine which one is the imposter of the group and defend their answer.
Description:
This activity is based off of the design of the book, Which One Doesn’t Belong?, by Christopher Danielson. Students are using mathematical reasoning of proportional relationships to find similarities and differences between the four representations of purple paint. There is no correct answer for this problem, as all of the pictures could be considered “imposters” based on different criteria. The emphasis, therefore, should be placed on the students’ reasoning of WHY a particular “imposter” was chosen.
The criteria for this problem focuses mostly on some common mistakes made with proportions:
- Not recognizing equivalent ratios
- Comparing measurements with different units
- Misapplying the parts-parts or parts-whole relationship
- Not simplifying ratios completely
This problem also includes multiple representations (picture, verbal, table and graph) that can be used to describe proportional relationships.
Teacher Instructions:
Step 1: Familiarize students to the overall idea of finding the imposter. Start by introducing a simpler example such as the following (bigger version available on the attachment):
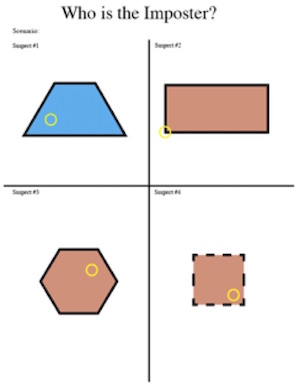
In this example, it is evident that any of them could be the imposter, as they all have at least one thing that makes them unique, and they all share some sort of commonalities with the other shapes. The goal, then, is for students to describe what characteristic makes each one unique. The following chart lays out some explanations of how each shape is unique (i.e., the “imposter”) but students might find more.
| Trapezoid | Rectangle | Hexagon | Square | |
| All shapes are red | Shape is blue. | X | X | X |
| All shapes have a circle inside | X | The circle is on the edge of this shape. | X | X |
| All shapes have 4 sides | X | X | This shape has six sides. | X |
| All shapes have solid lines | X | X | X | This shape has dotted lines. |
Step 2:
Introduce the paint example (see attachment). Allow students time, at first, to write down any observations that they have about the suspects. Encourage them to solve for any missing information that they can deduce about each “suspect.” As long as the statements are true, they can write them down.
- Is there any missing information that you can deduce?
- Are there any similarities/differences between the suspects?
- Extension: If you have already chosen one imposter, try to find a reason for another suspect to be the imposter.
Have students discuss their choices of imposter in groups. Then have the groups explain their reasoning to the class. There are many different ways that students can describe the imposters. Here are some possible characteristics:
| Picture | Words | Graph | Table | |
| All units have same labels | (Cups or Quarts needs Conversion) | X | X | X |
| All comparisons involve parts being compared to parts | X | The red paint (part) is compared to the purple (whole) | X | X |
| All ratios need simplification | X | X | Slope is 1/3 | X |
| All have equivalent ratios | X | X | X | (1/4, not 1/3) |
Step 3: As a class, write down mathematical reasons for labeling each example as an imposter.
Possible Follow-Up Questions:
- Use evidence to prove that all of these are proportional relationships.
- Which representation will create a different shade of purple than the others?